¶ Giant Vortex Clusters
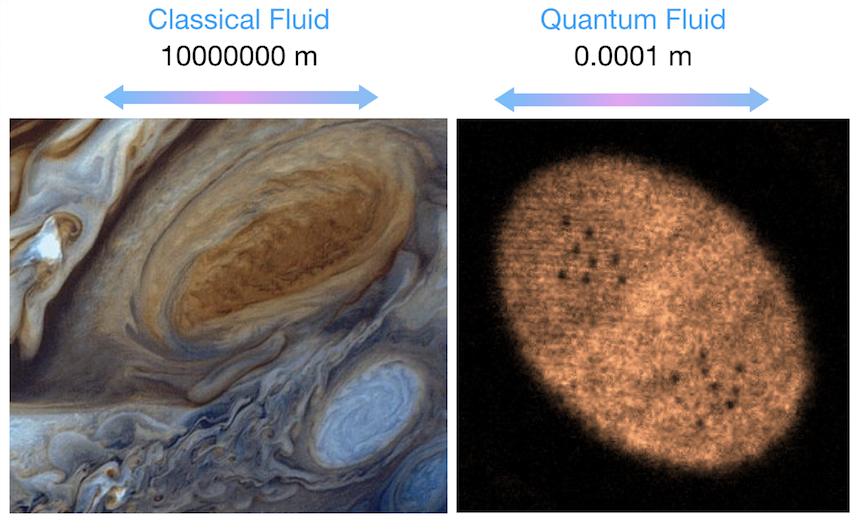
Our work on vortex clusters appeared in the July issue of Science. We report the first experimental observations of giant vortex cluster formation in a quantum fluid, confirming 70 year old predictions of Lars Onsager that ordered states can emerge at high energy in planar quantum turbulence. The giant clusters created form a quantum equivalent of large coherent structures emerging in planar turbulence, such as the famous Great Red Spot on Jupiter.
The experiment used state of the art laser manipulation to confine an ultracold superfluid, and then stir it in just the right way to inject giant vortex clusters without causing undue heating. Despite their high energy, these quantum storms were observed to be long lived, lasting for roughly 10 seconds.
Giant vortex clusters in a two-dimensional quantum fluid,
Guillaume Gauthier, Matthew T. Reeves, Xiaoquan Yu, Ashton S. Bradley, Mark Baker, Thomas A. Bell, Halina Rubinsztein-Dunlop, Matthew J. Davis, Tyler W. Neely, Science 364, 12664 (2019), arXiv
New findings on Fluid Turbulence, Ashton Bradley on Nights with Brian Crump, Radio New Zealand 2019
Order emerges from chaos in 2D vortices, Physics Today 2019
¶ Self-Bound Dipolar Droplets
Due to their long range anisotropic interactions, dipolar condensates support a rich phase diagram of interacting many body behaviour. In this theoretical work we show that dipolar condensate can be prepared into a three-dimensional wave packet that remains localized when released in free space. Such self-bound states arise from the interplay of the two-body interactions and quantum fluctuations. We develop a phase diagram for the parameter regimes where these self-bound states are stable, examine their properties, and demonstrate how they can be produced in current experiments.
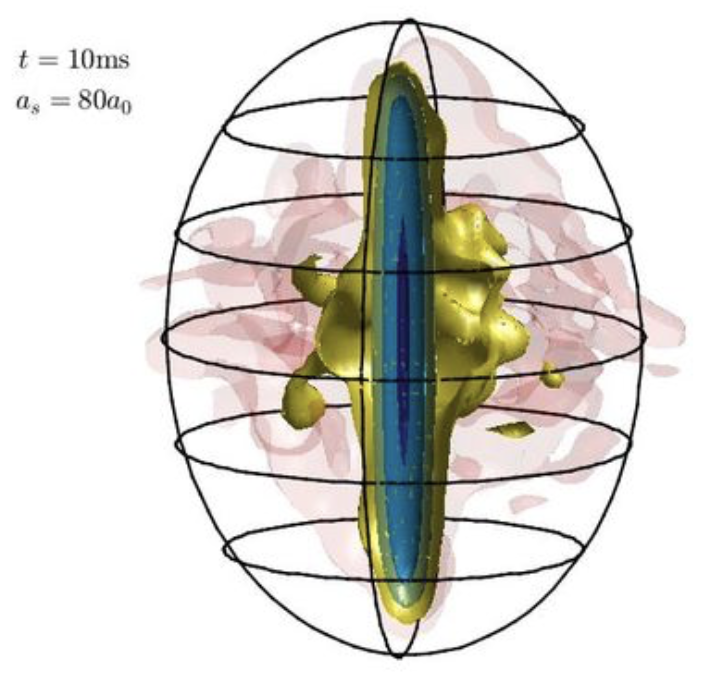
Self-bound dipolar droplet: a localized matter-wave in free space,
D. Baillie, R. M. Wilson, R. N. Bisset, and P. B. Blakie, Physical Review A (Rapid Communication) 94, 021602(R) (2016),
arXiv (Editor's Suggestion)
YouTube: Formation of a self bound dipolar droplet
¶ Superfluid Reynolds number
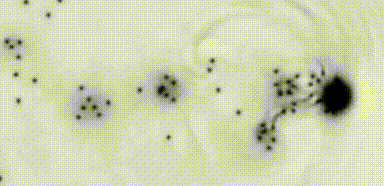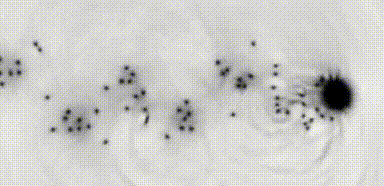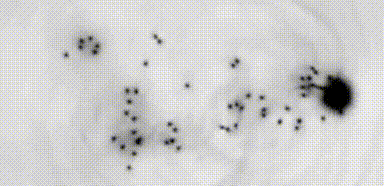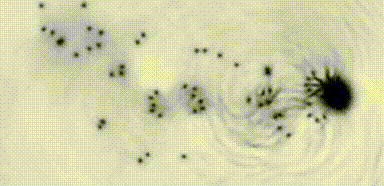The Reynolds number provides a characterization of the transition to turbulent flow, with wide application in classical fluid dynamics. Identifying such a parameter in superfluid systems is challenging due to their fundamentally inviscid nature. Performing a systematic study of superfluid cylinder wakes in two dimensions, we observe dynamical similarity of the frequency of vortex shedding by a cylindrical obstacle. The universality of the turbulent wake dynamics is revealed by expressing shedding frequencies in terms of an appropriately defined superfluid Reynolds number, , that accounts for the breakdown of superfluid flow through quantum vortex shedding. For large obstacles, the dimensionless shedding frequency exhibits a universal form that is well-fitted by a classical empirical relation. In this regime the transition to turbulence occurs at , irrespective of obstacle width.
Identifying a superfluid Reynolds number via dynamical similarity, M. T. Reeves, T. P. Billam, B. P. Anderson, A. S. Bradley,
Physical Review Letters 114, 155302 (2015) arXiv (Editor's Suggestion)
¶ Number Fluctuations of a Dipolar Condensate
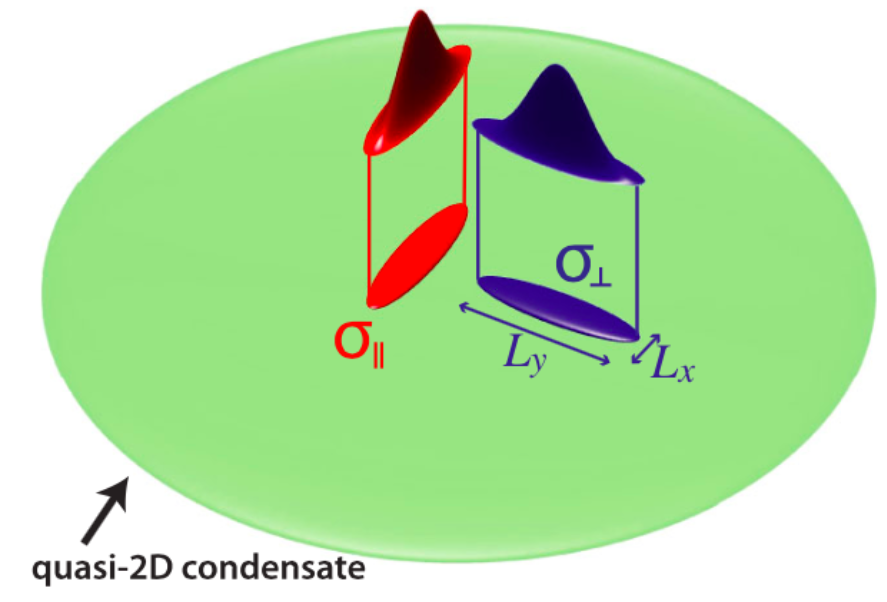We present a theory for the number fluctuations of a quasi-two-dimensional (quasi-2D) dipolar Bose-Einstein condensate measured with finite resolution cells. We show that when the dipoles are tilted to have a component parallel to the plane of the trap, the number fluctuations become anisotropic, i.e., depend on the in-plane orientation of the measurement cell. We develop analytic results for the quantum and thermal fluctuations applicable to the cell sizes accessible in experiments. We show that as cell size is increased the thermodynamic fluctuation result is approached much more slowly than in condensates with short range interactions, so experiments would not require high numerical aperture imaging to observe the predicted effect.
Number Fluctuations of a Dipolar Condensate: Anisotropy and Slow Approach to the Thermodynamic Regime, D. Baillie, R. N. Bisset, C. Ticknor, and P. B. Blakie, Physical Review Letters 113, 265301 (2014) arXiv